عنوانِ مقاله : اهله ی سیارات
نویسنده، عکاس و تصویرساز : محمد رنجبران
اهله واژه ای آشناست که بیشتر برای ماه به کار گرفته می شود. به معنیِ تغییرِ درصدِ روشنی سطحیِ ماه طیِ شبهای متمادی در یک ماهِ قمریست. این درصد روشنایی که در حالتِ کیفی، به فازِ ماه شناخته می شود، در دامنه ی هلالِ باریک شامگاهی، تربیع اول، هلال کوژ، بدر، هلالِ کوژ، تربیع سوم و هلال باریک صبحگاهی تغییر می کند، تصویر ۱.

تصویر ۱ : اهله ی ماهِ رمضان ۱۴۳۷
ممکن است یک ذهنِ کنجکاو در اینجا سوال کند که آیا برای سیاراتِ منظومه ی شمسی، که اغلبِ اوقاتِ سال در آسمان قابلِ رصد هستند، هم اهله وجود دارد یا خیر؟ برای دیدنِ این موضوع، به تصویر ۲ دقت کنید.

تصویر ۲ : (الف) هلالِ باریکِ سیاره ی زهره، ۵ خرداد ۱۳۹۹، (ب) هلال کوژِ سیاره ی مریخ، ۴ مرداد ۱۳۹۹
جوابِ ساده ی این سوال آری است. سیاراتِ درونی که زهره از جمله ی آنهاست، اهله را به طورِ کامل تجربه می کنند. اما، سیاراتِ بیرونی که مریخ ازجمله ی آنهاست، تنها بخشی از اهله را دارند.
به کمکِ هندسه می توان تا حدودی چگونگیِ ایجاد این پدیده را آشکار کرد. بدین منظور در تصویر ۳ به طور شماتیک، وضعیت نسبیِ زمین، خورشید و سیاره ی مریخ نشان داده شده است.
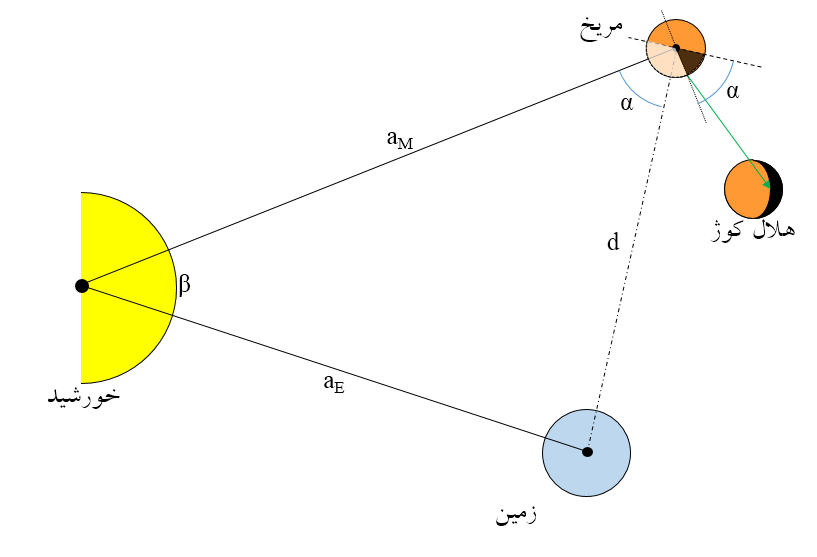
تصویر ۳ : مثلث فرضیِ بین خورشید، زمین و مریخ که در آن، ارتباطِ ظاهریِ زاویه ی سایه با فواصلِ خورشیدی به نمایش درآمده است.
گردشِ سیارات به دورِ خورشید از نمای بالایِ صفحه ی دایره البروج همگی به صورتِ پاد ساعتگرد است و به دلیلِ فاصله ی متفاوتشان از خورشید، دوره ی تناوب متفاوتی دارند. درصورتی که برای سادگی فرض شود مدار سیارات دایره است، می توان اندازه ی زاویه ی β را برحسبِ زمان، t، دوره ی تناوبِ زمین، TE، و دوره ی تناوبِ مریخ، TM، بدست آورد.

k در ترمِ آخرِ سمتِ راست، شماره ی تعدادِ دورهایی است که سیاره ی سریعتر، سیاره ی کندتر را پشتِ سر گذاشته است.
دقتِ بیشتر در تصویر ۳ آشکار می کند که برای یافتنِ درصدِ روشنیِ سیاره ی مریخ از زمین، لازم است که زاویه ی α محاسبه شود. اگر این زاویه صفر درجه باشد، به معنیِ بدر و اگر مقدار آن نزدیک ۱۸۰ درجه شود، به معنیِ هلالِ باریک است. معادله ی مربوط به درصد روشنی سطحی، تعاریفِ مختلفی دارد. یکی از این تعاریف استفاده از درصدِ روشنیِ مربوط به میانه ی سیاره است که رابطه ی آن چنین است.
 برای دستیابی به α، درگامِ نخست، با استفاده از قضیه ی کسینوسها، فاصله ی زمین و مریخ محاسبه می شود.
برای دستیابی به α، درگامِ نخست، با استفاده از قضیه ی کسینوسها، فاصله ی زمین و مریخ محاسبه می شود.

در گامِ دوم، ازنو قضیه ی کسینوسها نوشته می شود. اما، این بار برای زاویه ی α.
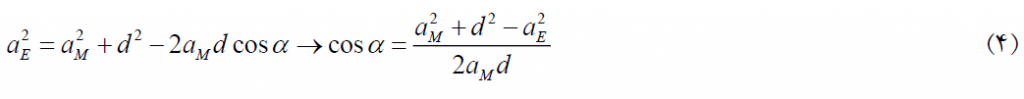
در گامِ سوم، با جایگذاریِ d از معادله ی (۳) در رابطه ی (۴)، فرمولِ محاسبه ی درصد روشنیِ سطحی چنین خواهد شد.
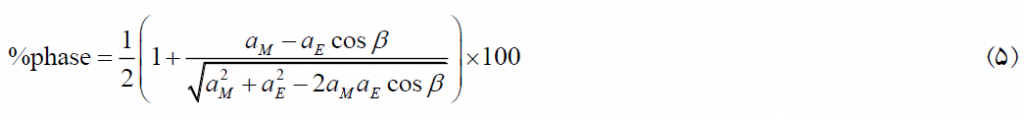
حسنِ معادله ی (۵) در این است که مستقل از زمان است. درنتیجه، تنها با تغییرِ زاویه ی β بین صفر تا ۳۶۰ درجه، می توان به دامنه ی تغییراتِ درصد روشنیِ سطحی، تصویر ۴، دست یافت.
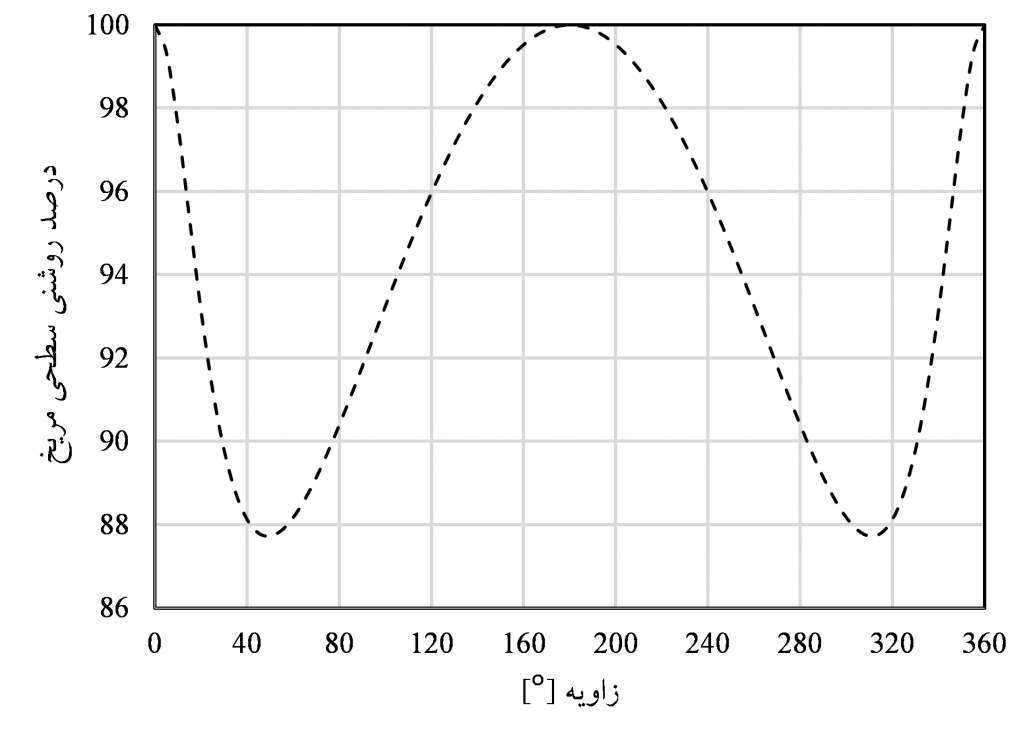
تصویر ۴ : درصد روشنیِ سطحیِ سیاره ی مریخ بر حسبِ زاویه ی β، معادله ی (۵).
حسن دیگرِ معادله ی (۵) در این است که نه تنها برای سیاره ی مریخ قابل استفاده است، بلکه می توان براحتی آن را به سیاراتِ دیگر هم تعمیم داد. تنها لازم است که بجای aM از فاصله ی خورشیدیِ باقیِ سیارات استفاده شود و رفتار آنها را دید، تصویر ۵.
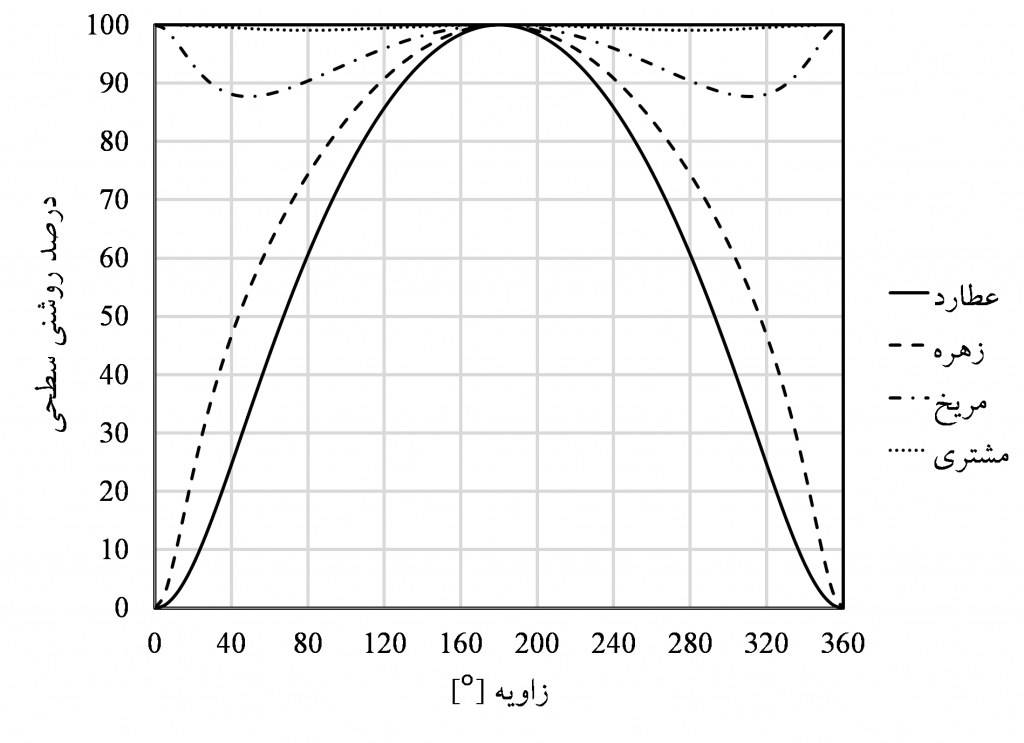
تصویر ۵ : مقایسه ی تغییراتِ درصد روشنی سطحی عطارد، زهره، مریخ و مشتری با استفاده از معادله ی (۵).
همانطور که در تصویر ۵ هم دیده می شود، دو سیاره ی درونی، عطارد و زهره، می توانند کل دوره ی هلالی را از صفر تا ۱۰۰% تجربه کنند. اما، برای سیاراتِ بیرونی، دراینجا مشتری و مریخ، حدی وجود دارد. همچنین، برای سیاراتِ دورتر از مشتری هم کاهش در صد روشنی سطحی کاملا قابل چشم پوشیست.







دیدگاهتان را بنویسید